Euclid Tougher than Minkowski

We've done a few Geometry Expressions demos showing off Minkowski geometry and how it solves problems in Special Relativity. How about Euclidean geometry? The usual 2D rotation diagram is easy enough to set up. Let point B have coordinates x,y. Let the red frame be rotated by angle theta with respect to the blue frame and ask "What are the coordinates of B in the red frame?" We all remember the answer: x' = x cos theta + y sin theta, y' = - x sin theta + y cos theta. What does GX say?


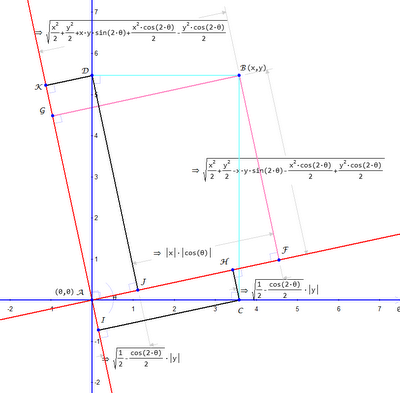
JF is obviously (BD = x) cos theta, as is IC = (AC = x) cos theta, just by looking at the picture. Ditto HF = (BC = y) sin theta, and the y' coordinate is just as easy to see. Mathematica's simplification machinery is better than GX's, and it's a simple matter to copy-as and paste back to Mathematica,


I'm getting quite accustomed to this procedure. It's amusing as well as useful.

GX file for you to download is at http://home.comcast.net/~brianbec/Euclidean3.gx